Check the alignment of harvester and applicator/planter for mixed treatment problems where multiple input rates are associated with yield monitor data
Examples
#--- load trial design ---#
data(td_single_input)
#--- check the alignment of harvester and applicator/planter ---#
machine_alignment <- check_alignment(td_single_input)
#--- check the degree of mixed treatment problem ---#
machine_alignment$overlap_data
#> [[1]]
#> ha_strip_id strip_id area ha_area total_intersecting_ha_area
#> <int> <int> <num> <num> <num>
#> 1: 7 1 4802.128 4914.658 4802.128
#> 2: 8 1 4802.216 4914.095 4802.216
#> 3: 9 1 4800.159 4913.532 4801.744
#> 4: 10 2 4800.448 4912.968 4800.510
#> 5: 11 2 4800.559 4912.405 4800.559
#> 6: 12 2 4798.673 4911.842 4800.955
#> 7: 13 3 4798.842 4911.279 4798.946
#> 8: 14 3 4798.867 4910.715 4798.867
#> 9: 15 3 4796.282 4910.152 4798.333
#> 10: 16 4 4797.150 4909.589 4797.174
#> 11: 17 4 4797.210 4909.025 4797.210
#> 12: 18 4 4795.219 4908.462 4797.983
#> 13: 19 5 4795.517 4907.899 4795.556
#> 14: 20 5 4795.519 4907.336 4795.519
#> 15: 21 5 4793.429 4906.772 4795.620
#> 16: 22 6 4793.753 4906.209 4793.800
#> 17: 23 6 4793.793 4905.646 4793.793
#> 18: 24 6 4791.617 4905.082 4793.897
#> 19: 25 7 4792.114 4904.519 4792.184
#> 20: 26 7 4792.136 4903.956 4792.136
#> 21: 27 7 4789.221 4903.392 4791.600
#> 22: 28 8 4790.392 4902.829 4790.416
#> 23: 29 8 4790.411 4902.266 4790.411
#> 24: 30 8 4787.375 4901.703 4790.130
#> 25: 31 9 4788.742 4901.139 4788.785
#> 26: 32 9 4788.719 4900.576 4788.719
#> 27: 33 9 4785.993 4900.013 4789.221
#> 28: 34 10 4779.629 4897.277 4779.629
#> 29: 35 10 4779.652 4892.002 4779.652
#> 30: 36 10 4777.767 4886.723 4779.512
#> 31: 37 11 4763.732 4881.445 4763.820
#> 32: 38 11 4763.784 4876.166 4763.784
#> 33: 39 11 4761.437 4871.850 4763.524
#> 34: 40 12 4756.581 4870.037 4756.611
#> 35: 41 12 4756.612 4868.388 4756.612
#> 36: 42 12 4754.252 4867.832 4756.389
#> 37: 43 13 4755.735 4867.802 4755.755
#> 38: 44 13 4755.800 4867.771 4755.800
#> 39: 45 13 4754.043 4867.741 4756.146
#> 40: 46 14 4755.675 4867.710 4755.753
#> 41: 47 14 4755.733 4867.680 4755.733
#> 42: 48 14 4753.699 4867.649 4756.390
#> 43: 49 15 4755.654 4867.619 4755.702
#> 44: 50 15 4755.632 4867.588 4755.632
#> 45: 51 15 4753.589 4867.557 4756.247
#> 46: 52 16 4755.582 4867.527 4755.651
#> 47: 53 16 4755.564 4867.496 4755.564
#> 48: 54 16 4752.952 4867.466 4754.947
#> 49: 55 17 4755.394 4867.435 4755.396
#> 50: 56 17 4755.429 4867.405 4755.429
#> 51: 57 17 4752.843 4867.374 4754.830
#> 52: 58 18 4755.301 4867.344 4755.321
#> 53: 59 18 4755.396 4867.313 4755.396
#> 54: 60 18 4753.484 4867.283 4756.029
#> 55: 61 19 4755.245 4867.252 4755.335
#> 56: 62 19 4755.295 4867.222 4755.295
#> 57: 63 19 4753.394 4867.191 4753.394
#> ha_strip_id strip_id area ha_area total_intersecting_ha_area
#> intersecting_pct dominant_pct
#> <num> <num>
#> 1: 0.9771030 1.0000000
#> 2: 0.9772331 1.0000000
#> 3: 0.9772490 0.9996699
#> 4: 0.9771098 0.9999872
#> 5: 0.9772318 1.0000000
#> 6: 0.9774245 0.9995247
#> 7: 0.9771277 0.9999783
#> 8: 0.9772237 1.0000000
#> 9: 0.9772270 0.9995726
#> 10: 0.9771030 0.9999950
#> 11: 0.9772225 1.0000000
#> 12: 0.9774921 0.9994238
#> 13: 0.9771099 0.9999919
#> 14: 0.9772143 1.0000000
#> 15: 0.9773471 0.9995431
#> 16: 0.9770884 0.9999902
#> 17: 0.9771993 1.0000000
#> 18: 0.9773326 0.9995243
#> 19: 0.9770956 0.9999854
#> 20: 0.9771980 1.0000000
#> 21: 0.9772011 0.9995034
#> 22: 0.9770717 0.9999950
#> 23: 0.9771829 1.0000000
#> 24: 0.9772380 0.9994249
#> 25: 0.9770759 0.9999909
#> 26: 0.9771748 1.0000000
#> 27: 0.9773895 0.9993260
#> 28: 0.9759769 1.0000000
#> 29: 0.9770339 1.0000000
#> 30: 0.9780606 0.9996349
#> 31: 0.9759038 0.9999814
#> 32: 0.9769529 1.0000000
#> 33: 0.9777650 0.9995618
#> 34: 0.9767093 0.9999938
#> 35: 0.9770405 1.0000000
#> 36: 0.9771063 0.9995506
#> 37: 0.9769821 0.9999957
#> 38: 0.9769975 1.0000000
#> 39: 0.9770748 0.9995578
#> 40: 0.9770001 0.9999835
#> 41: 0.9770021 1.0000000
#> 42: 0.9771431 0.9994344
#> 43: 0.9770080 0.9999899
#> 44: 0.9769997 1.0000000
#> 45: 0.9771321 0.9994413
#> 46: 0.9770158 0.9999854
#> 47: 0.9770042 1.0000000
#> 48: 0.9768834 0.9995805
#> 49: 0.9769818 0.9999996
#> 50: 0.9769948 1.0000000
#> 51: 0.9768778 0.9995821
#> 52: 0.9769848 0.9999959
#> 53: 0.9770063 1.0000000
#> 54: 0.9771425 0.9994651
#> 55: 0.9770060 0.9999812
#> 56: 0.9770039 1.0000000
#> 57: 0.9766195 1.0000000
#> intersecting_pct dominant_pct
#>
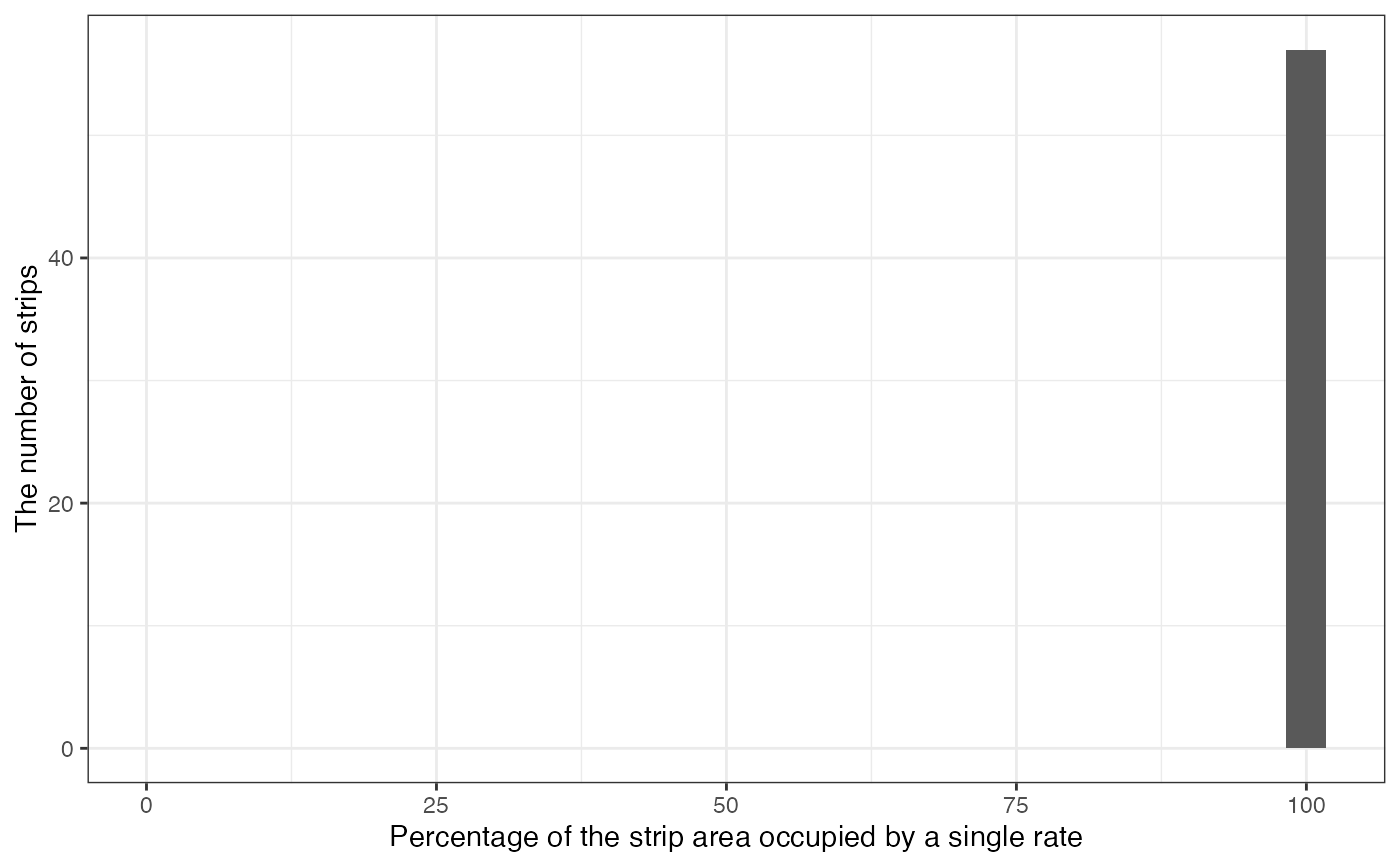
#--- visualize the degree of mixed treatment problem ---#
machine_alignment$g_overlap[[1]]
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
#> Warning: Removed 1 row containing missing values or values outside the scale range
#> (`geom_bar()`).